How to Calculate Integral in Excel
Integral is one of the most important tools in mathematics. It can be used to calculate area, volume, and many other useful parameters. In this blog, we are going to discuss the methods of calculating integrals in Excel.
The Concept of Integral
In calculus mathematics, there are two main operations: integration and differentiation. Integral is the inverse operation of differentiation. Integration is a way of adding slices to find the whole. Its most common use is the calculation of the area under a curve.
There are two types of integrals: definite and indefinite integrals. In an indefinite integral, you must have the function F formula to calculate its integral, which gives F when it’s differentiated. If you want to calculate Integrals with Excel, forget indefinite integral because it’s a matter of analytical calculation.
Definite integral relates to numerical values. It is used in applied mathematics, statistics, science, and many more. It can be calculated using indefinite integral and numerical methods.
Methods of Calculating Integral
When it comes to integration, you may face two situations: you have an equation to integrate or a corresponding x and y values. As we discussed earlier, Excel can not integrate using analytical methods. So, in any case, you will have to turn the equation into numbers.
Based on numerical mathematics, we can calculate an integral via two methods derived based on the calculation of the area of geometric shapes.
Trapezoidal Method for Calculating Integral
This method assumes that the area under a curve consists of several trapezoids. The area of a trapezoid can be calculated using the formula below:
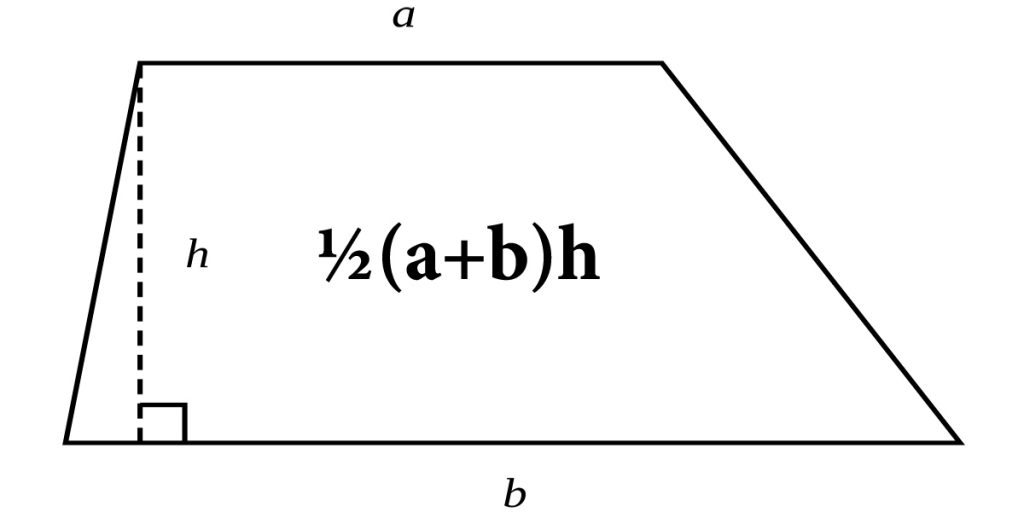
Now, all we have to do is add up the area of these trapezoids to calculate the integral.
Assume that we have a dataset of (x,y) related to each other with the F function.
y=F(x)
F can be any function. To calculate the integral by this method, we add up the area under the curve between all consecutive points.
Example: calculating integral of a function
We are asked to calculate the integral below:
Follow the steps below:
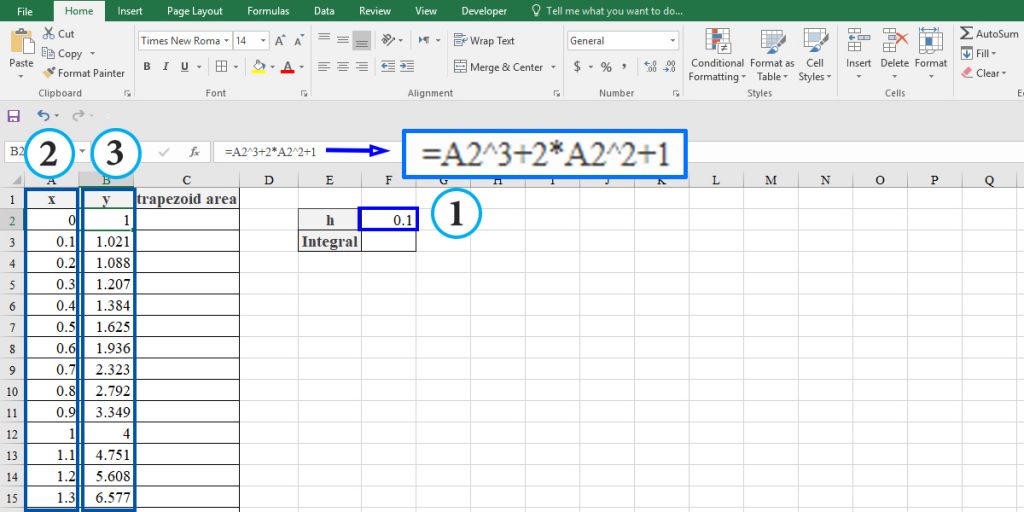
- Set the dx value, which is the height of the trapezoids. Let’s call it “h.” and set it 0.1 in this example.
- Set x values from 0 to 2 with a step of the desired “h.”
- Calculate y values using the function formula.
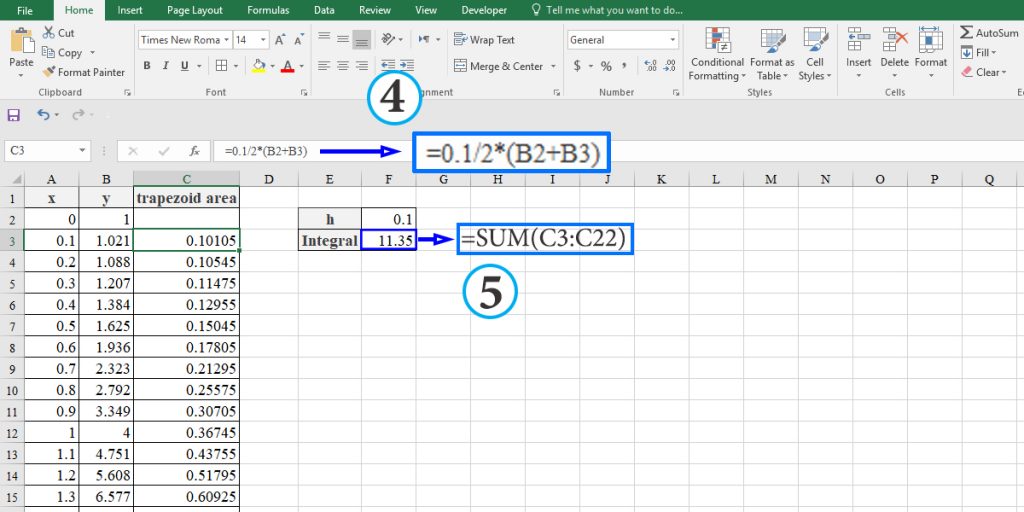
- Type “=0.1/2*(B3+B2)” in cell C3 and press Enter. Then click on the little box in the bottom right corner of the cell and drag it to the last point (cell C22).
- Now, add up the area value of all trapezoids using the SUM function.
Note: The lower the dx, the more accurate will be the result.
Example: Calculating the area under a curve when the function is not available.
In this example, we want to calculate the area under a curve. As we discussed earlier, integration is the way.
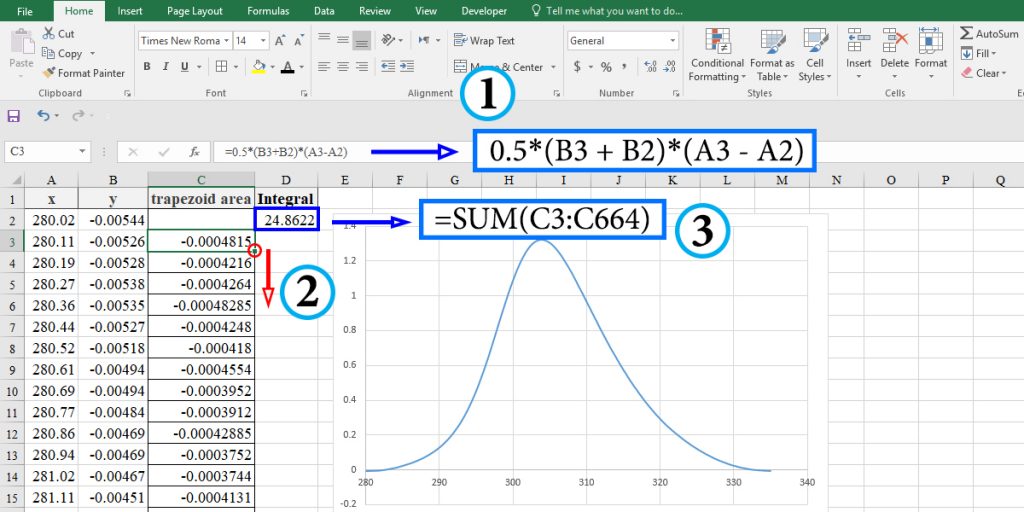
Here, the ∆x is not constant. So we can not set a dx; instead, we use the difference between two consecutive x values as the height of the trapezoid. Now, let’s calculate the integral by following the steps below:
- Type “0.5*(B3+B2)*(A3-A2)” in cell C34 and press Enter.
- Click on the little box in the bottom right corner of the cell and drag it to cell C, which is the cell containing the end point.
- Calculate the sum of the totals in Column C.
The Simpson Method for Calculating Integral
The Simpson method assumes that the area under the curve is formed by adding several parabolas. Before using this method, you have to make sure that you have an odd number of data points. It may be useful to mention that the Simpson method is more accurate than the trapezoid method for calculating the integral.
If the function that relates y to x is y=f(x), the formula for calculation of the integral is as below:
This formula gives the area for three consecutive points as a single parabola. To calculate an integral, we have to sum the area under the curve for all the parabolas. So, the resulting formula would be:
Now, let’s use it to calculate an integral.
Example: We want to calculate the following integral.
Follow these steps:
- First, we have to turn the function to numbers and set the dx (or h). If you have an x and y values dataset, check if the difference between x values is constant. If it’s not, you can calculate the average of ∆xs as “h.”
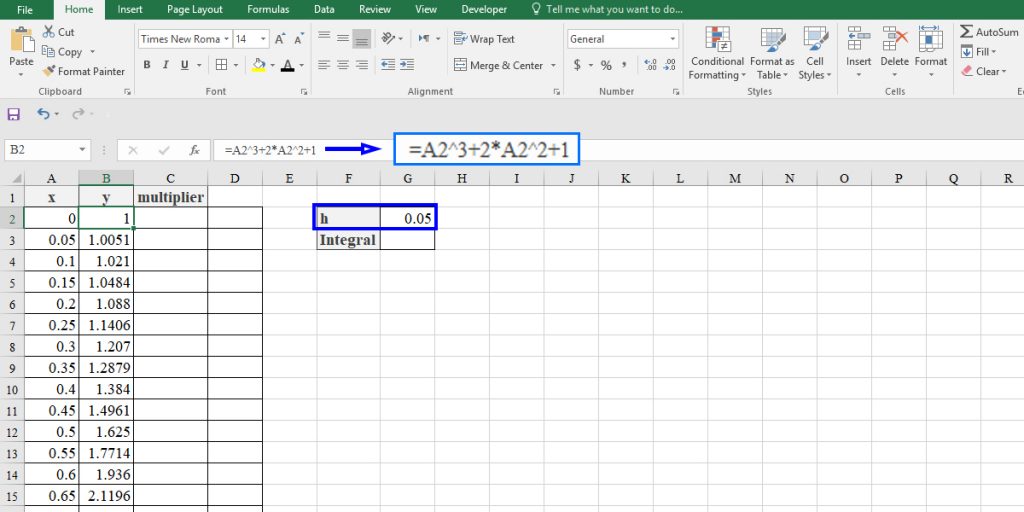
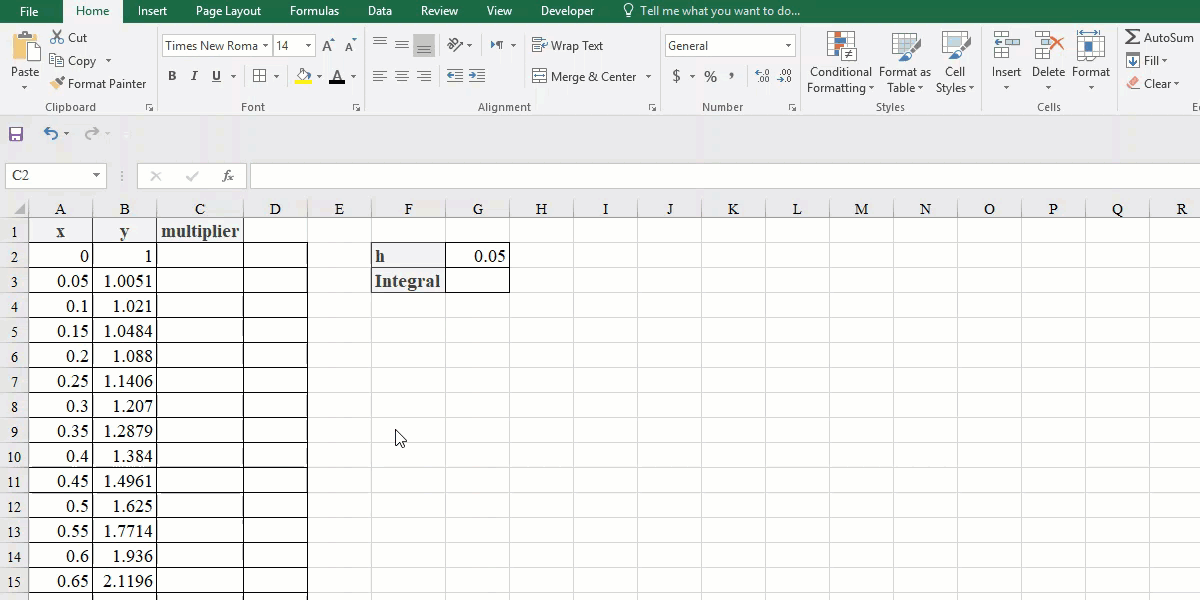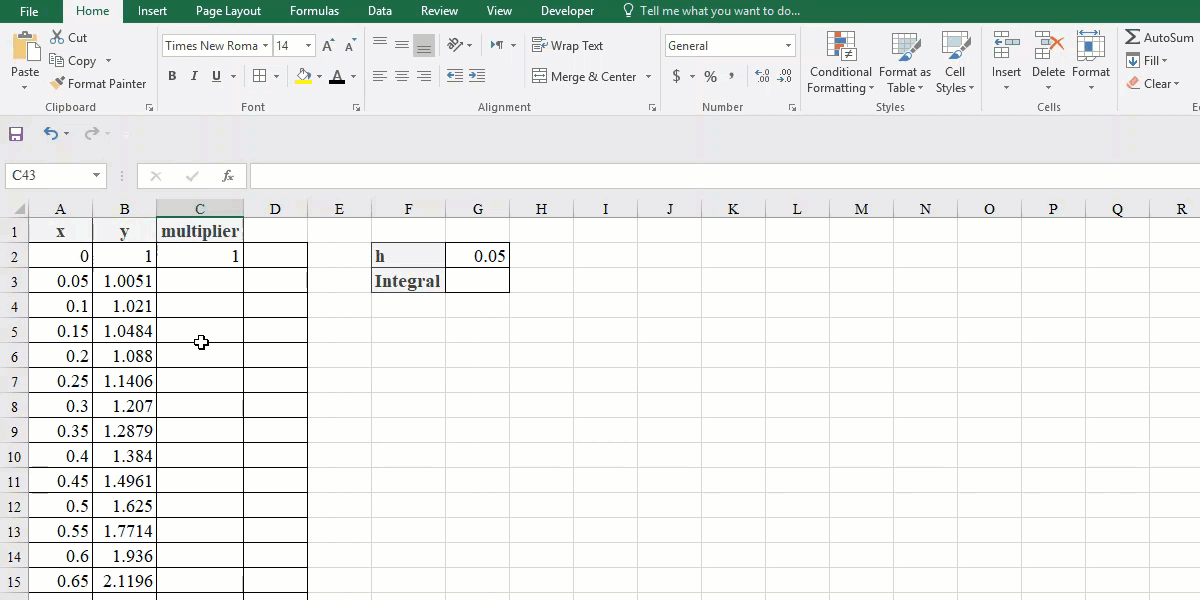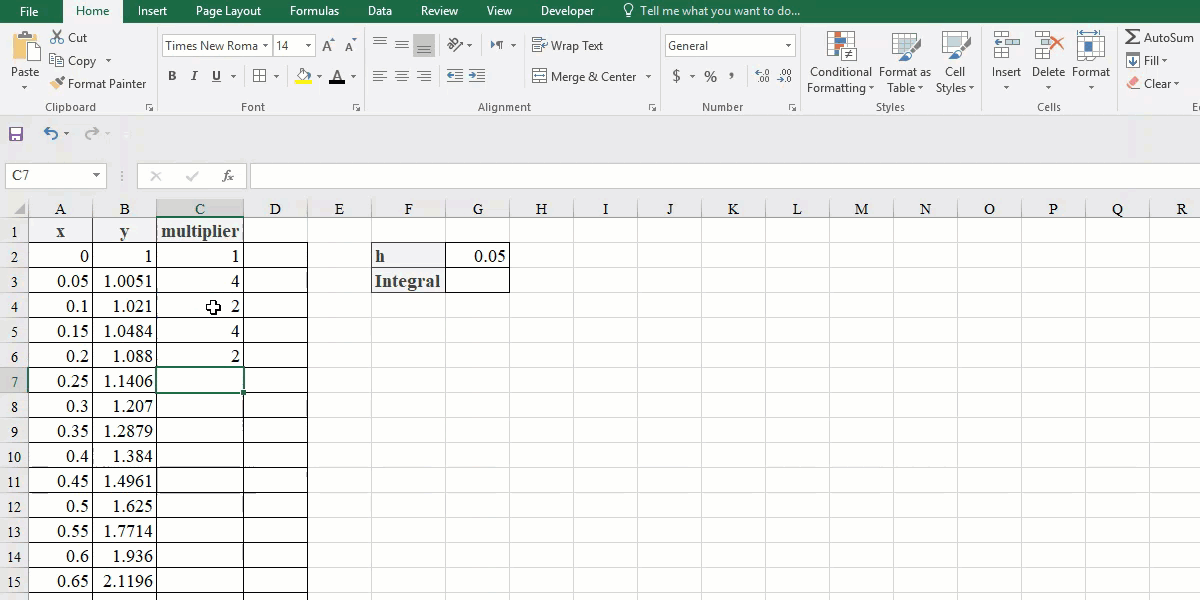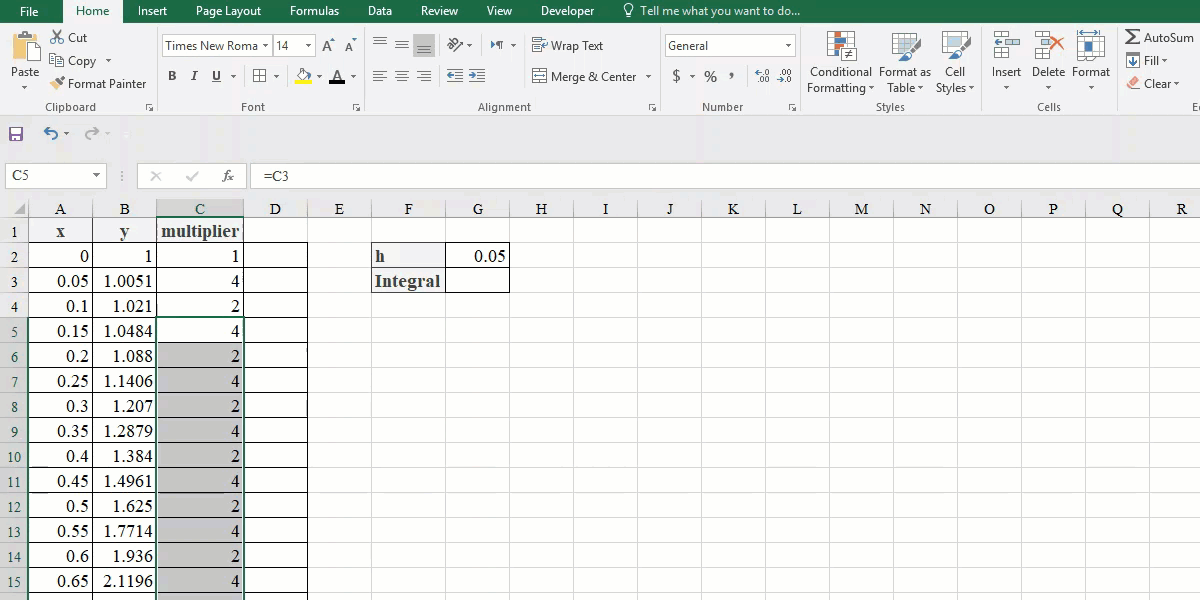
- We have to set the multipliers for each y value. The first and the last ones are 1. Type 4 in the cell C2 and 2 in the cell C3.
- Enter “=C2” in the cell C4 and “=C3” in the cell C5. You can select these cells by clicking, too. Then drag these two entries down to the second last point.
- In cell D2, type “=B2*C2” and press Enter, then drag it to the last point.
- Type “=1/3*G2*SUM(D2:D42)” and press Enter
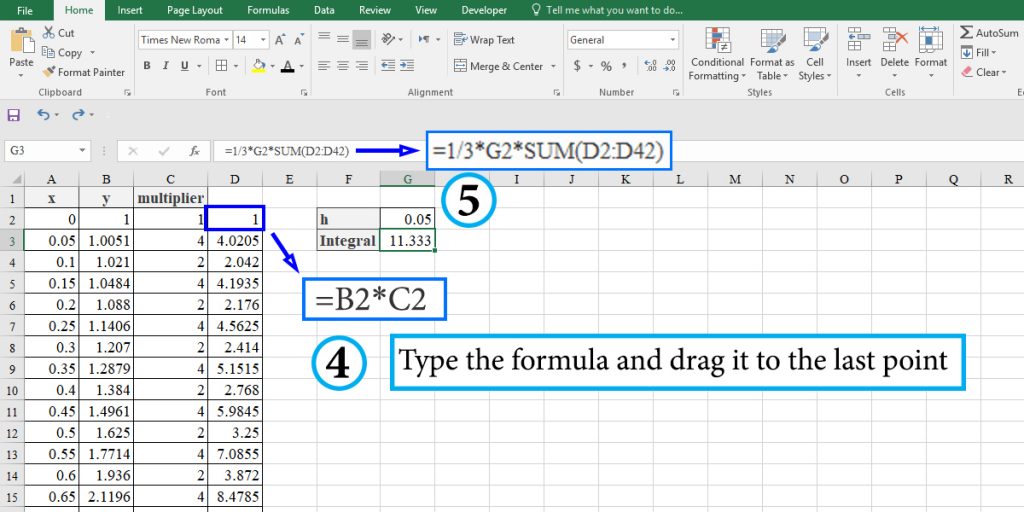
Note: While calculating the integral of a function, the smaller the ∆x (or h), the more accurate result you will have.
If you’re specifically interested in determining the area under a curve using Excel, you might also find our guide on calculating area under a curve helpful.
Bottom Line
We explained two methods for integration in Excel, based on numerical mathematics. You can apply these methods to the problem you may encounter.
You can connect with our experts, make inquiries, and get more Excel Support services.
Reduce cost, accelerate tasks, and improve quality with Excel Automation Services.
Our experts will be glad to help you, If this article didn’t answer your questions. ASK NOW
We believe this content can enhance our services. Yet, it’s awaiting comprehensive review. Your suggestions for improvement are invaluable. Kindly report any issue or suggestion using the “Report an issue” button below. We value your input.